[email protected]
立即下单
24小时全年无休客服

wechat

本公司旗下写手皆为公司直聘 网络写手勿扰
案例中心
MA 3502 Regression Analysis and Experimental Design
创建日期：2024-06-22 15:23:34
所属分类：数学mathematics
标签： MA 3502
Regression Analysis and Experimental Design

Hello, dear friend, you can consult us at any time if you have any questions, add  WeChat:  THEend8_


MA 3502 Regression Analysis and Experimental Design

Structure of Examination Paper:

There are Five pages.

There are FOUR questions in total.

There are no appendices.

The mark obtainable for each question is 25.

Instructions to Students :

Answer FOUR questions.

Show clearly all your workings.

In all exercises, dj is the j-th digit of your student number.

Question 1.

1a. Consider the linear regression model Y = Xθ+ε, where θ is an m-vector of unknown parameters, Y is an N-vector of observations, X is a design matrix of size N × m and ε is a vector of normal random errors with mean 0 and covariance matrix σ2IN . Here σ2 is some positive unknown constant and IN is the identity matrix of size N × N. Assume that rank(X) = p ≤ m.

(i) Give a geometrical interpretation of the LSE, the least squares estimator (LSE) of θ.

(ii) Defifine the lasso estimators of θ and discuss a motivation behind these estimators.

(iii) Defifine the ridge estimator of θ and brieflfly discuss its properties.

(iv) Let Z be a vector of size m such that the linear form ZT θ is estimable. Explain the method of constructing confifidence intervals for ZT θ.

(v) Derive the maximum likelihood estimator for σ2.

[10=2+2+2+2+2]

1b. Assume m = 3, N = 5 and the model yj = θ0 + θ1xj + θ2x2j + εj . The table below displays the design points and the corresponding results:

xj 0 u −u v −v

yj 0 1 −1  1 −1

Here u = d4 + 1 and v = d4 + 2, where d4 is the fourth digit of your student number.

(i) Test the hypothesis that the complete regression model is statistically signifificant on the 95% confifidence level. Write down the corresponding ANOVA table and compute R2.

(ii) Test the hypothesis

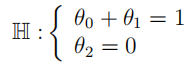
on the 95% confifidence level.

To answer this question please use 19.0 as an approximate value for the 0.95-quantile of the F-distribution with 2 and 2 degrees of freedom.

[15=7+8]

Question 2.

2a. Consider the linear regression model Y = Xθ+ε, where θ is an m-vector of unknown parameters, Y is an N-vector of observations, X is a design matrix of size N × m and ε is a vector of normal random errors with mean 0 and covariance matrix σ2IN .

In a particular application, m = 4, N = 5 and the model is Y = θ1X1 + θ2X2 + θ3X3 + θ4X4 + ε. The table below displays the design points and the corresponding results

X1 u   -1  1  0 -1

X2 −v   1  0  1 -1

X3 u−v  0  1  1 -2

X4 u+2v  -3  1 -2 1

Y   1  1  1 -1  0


案例分类
标签云
关键词一 关键词二 关键词三 关键词四 关键词五 和法规和的发更好的风格和 ECON 615 FINC 612 CSC148 COMP 639 ACCT 203 ACCT 211 PSYC 101 MTH2009 COMP52315 PSYCO 432 statistics MATH4063 11 xxx 1 MA1MSP MAST30028 MATH3888 CS341 EEE30002 ES2F5 MCD4160 CC0933 ECON 1101 MCHM3001 CHEM3118 COMMGMT 2511 COMP41280 STAT 631 24T1 IRE379 SENG365 ECON433 FIT3139 MATH4602 LING5621M FINS5516 ECON3208 MN2177 L2 SM EEET1415 Finance DS4023 COMP3004 7CCSMRTS K1S5B6 Stat230 CSCI4211 CSI2132 ECON30130 MAS6100 ENVS222 COM2107 INFO1112 STAT 4004 FIT2100 comp2022 COMP4691 Physics 307 Econ 659 probability CSCI316 fir29 CSCI203 COMP3160 COMP6714 INFO1113 Physics 7B Physics Photonics S203031 STAT2005 COMP90015 CSCI 2110 CSCC46 Information CSC477 COMP4650 Statistical COMP 346 COMP1017 ELEC340 MATH1007 Programming function STAT 244 CS 134 Java cse13s Math 108A FW20 ECON3389 CSE 130 Science 331 COMP9020 engineering COSC 445 CSE 5523 GAME2012 visualization MATH 235 Math 370 CSC343 COGS 108 EE524 COMP10200 STAT 416 3FK4 MSCI 311 ECON6113 ACC40700 EMESTER1 MAS8383 ECO 512 STAT 8310 CMN3102 MA577 CMPT 225 COMP0045 Methods Equations MATH 113 Math 3283W ICS-33 EN4302/ENT603 BIA B350F MA318 MTHM506 MECH 5315M ECONOMICS MAS8382 COM 2004 PX3142 XJEL 3662 STAT 231 MGT B399F PX4131 COM2108 30AM MSCI521 ECONM1015 ACFI304 GR5241 MATH10101 ECON 2070 COMS31900 EFIM20011 CSE 250B ACSE-5 STAT4207 SOFT2412 ELEC 331 AY2020 MSIN0209 FIT2094 CS 241L ST404 CS 411 3D CA3 INF4002 COMP3506 SIT718 CS 188 CS 170 MATH 138 CSE 251A CMT118 DATA5207 CMPT307 CMPT459 T1 PGEE11108 COSC 3P32 ME 163 MATH96007 7QQMM203 EE6227 BA 574 STA 4234 ECO206Y1Y ECO2008 MT2300 MATH 11158 CS 527 MACM 316 CSE474 2DI70 ISE 525 COMP3411 EMAT30007 7CCSMBDT MFIN704 MFIN704W21 MfIB ECE 438 CS 436 F36 CS5344 FE 621A FE621 TBA 612 ECM3151 ECMM422 MF1 MSIN0107 ESSMENT CS 5854 MFIT 5008 MIPS R4000 ENG5274 BU52018 ENG2079 BIOA02 STA2570 F0 INF553 STAT 440 STAT3008 COMP9417 COMP6451 6COM1042 BU52006 ST303 HW-1 CISC-235 CS 510 MATH3161 ECN 140 ECE391 Comp 3613 CVEN 9625 PRG455 UESTION 1 EARN 5 FE 825 IERG 5130 STAT 8178 EE161 ADS2 G54FUZ CS326 113B ECN 226 QBUS6860 ELEC3202 COMP9334 MGT11B MET CS 777 STA238 00099F Python SMM306 CMT206 EC116 SP MAST90084 CS480/680 BCPM0091 CMPT 300 ECON2209 FY20 STAT 432 CVEN9625 MATH1712 CMP9771M CMP3750M CIS 325 AI506 MAT344H1S MGT7180 PSTAT 160B CSYS5010 1D STAT 453/558 ME152B STA304H1F CSCI-128 ME428 CO3002 FINE 7640 COMP3234 ECSE 223 EE497 – 3D MATH5905 ECS648U ENG5009 MATH10242 EC665 A CPI221 ISOM5220 MACE40402 MGT B456F COMP9315 AFM 113 STAT 778 CS 564 MA231 CS 230 CS 124 COMP5511 CSC317 ITEC1010 ELEC207 INFT 3019 7CCMFM06 EE 161 5G ECLT5810 MATH 7349 CS526 O2 COMP90054 ELE00063M ACCT5034 ARC1015 CSCI 40 CSCI E40 FIN 524B CS 462 389COM CMT309 MFIN703 COMP4250 STA304 STA304H1S STA 1003 FIN 448 BUFN 732 CS520 CVEN3701 ECMT6006 PHAS0100 CSIT314 MDIA 5028 CSCI 2134 MAT 451 CMPT 459 STAT 457 INFO20003 COMP4141 IELE8066 F540 ECM9 CSE 6321 FIN 430 MATH3911 BFC5916 COMP1011 EEE 6209 STATS 240 CW3 COMP206 COMP1003 4331W ISE 530 CMPT 295 MATH 239 QF5203 INFR08010 IT114105 FIT2093 ECON3124 ECON1195 MATH 337 STAT 3006 COMP202 COMP3130 MATH3609 COMP 250 CS6140 IEEE ELE00041I FIN40090 CIV 5899 MATH3066 IGNMENT MATH 2009 STAT3405 HIST 101 MATH 3281 CEGE0042 ICT532 LAB 7 LAB 5 MCO455 CSIT214 Q4 IFB104 A1 ECO220Y5Y DA5020 CMPSC473 FIN9007 DSCI553 MSCI534 COMP3308 CSE-112 CMPT 310 EE104 F 2C P20 ALY2010 BUSM060 STA258 ECO00030M R BIOSTAT 274 COS6012-B FIT3155 CMPUT 340 EC421 INFS4205 ECOM135 NATS 1740 COMP809 MBE 6005 STA465 CSSE2310 CIVL2700 DATA4700 CMPSC 473 ISE 529 CS5044 MAST30020 COMP2207 ENGG1001 COMP0046 FIT3165 STAT GR5241 MECH0007 vATHK1001 ANALYTIC ATHK1001 MATH352001 HW3 S1 BMAN 24662 COMP 636 Stat-461 STAT 302 STAT 2132 STAR534 ENG4137 CMP3752M CS3103 BISM3222 STA 135 ME155A IIMT3601 ECON3371 ECON 3371 HW4 FINA 5840 DT211C CTEC3902 MAT005 MATH2148 S261F Econ 332 MATH3734 MIS41270 7CCMFM13 SYST 664 CIS434 CENG10014 MT4111 MT4527 ECMM424 CMT219 Math 136 MATH 3120 COMP10002 MAST20009 MATH0058 BEEM117 ISYE 6420 MGMTMFE 405 25579 1ECE 273 M122 COMP4434 1ELEC ELEC5620M STAT0010 BFF2401 MXB361 MATH3811 CS330 CMT307 FIT1033 CptS 583 UP 431 MATH6005 AF5343 CS2435 ECOM30002 ES50061 CS 2506 ECMT6002 CODE 00099F MT4539 ESSAY ICM317 MATH1231 MFIT5010 BMA547 MATH334 CIVL2201 MATH39032 T-04 CIVE97119 EMESTER CAB302 CAB301 59PM STAT802 ISYS3412 RM3 COSC 2123 AcF 311 MATH2022 1FINAL 4CCS1PHC ICM 142 ENVS3023 Math 4023 I1 ACSE8 FIN B385F CS-275 STA 4109-01 A31021 EE140 MT1 EE124 ECO-6004B Inf2-IADS CS126 IS2184 UL18 MATH5092 ECOM009 COMP 6211 ELEC202 MKT3019 IAB230 FIT5046 584-S21 COMP3210 CO250 A29401 MATH 136 MGT6174 ECMT6007 DATA2001 MAT 443 MATH10222 PHDE0071 ELE00123M COSC1295 MAT00045H MATH32032 1004GRC MAS223 COMP10001 DATA3404 CIVL2110 STAT2008 FNCE10002 EEE6431 COM6515 COMP9120 NBS8185 ECTE942 ECON 405 MATH314301 STAT 2011 COMPSCI 350 COMP20007 CMPSC-132 ECON5002 STA 35 MTH6108 FIT5147 MTH6150 100C FINA 5260 DESC9115 ECON4998 NBS8257 GMM ECON 6070 BSA2 ECE599 STATS 102B STA120 INFS601 BFC3241 MATH20602 COMP532 MAS275 COMP5318 COMP4002 FIT5086 MAST20004 FIT3152 FIT5129 CIS2380 CS521 COMP 1005 EECMS CITS5501 ECE 462 ECON 6002 ENG 4051 CSC 648 CMT654 MECHENG 713 PHYS1002 AMME 2000 FP0060 DDES3200 MECHENG 743 BINF90002 FIT2081 ISYS90081 ELECTENG 722 BUS 360 ECOS3010 BUS2810 ETF2100 ENG2048 STAT5002 COMP2017 CEME 2003 MATS3004 COMP9319 PHYS1001 COMP5349 AMME2261 COMP-381 FIT3173 COSC2757 ENG4025 QBUS2820 COMP9414 MATH2021 EOSC118 MFIN6690 PMATH 321 CSE-141L MATH575A COMPSCI5002 COMP1511 management comp2123 FINS3616 COMP 3331 COMS30034 DTSC 71 AcF 702 AcF702 DTSC71 MAT021 ELE8083 ACFI213 EG-127J 127J FIT5163 FIT2001 ELE00113M CMT310 CS 245 ENGL 1101 MTH6115 EE497 CS 325 Math 124A MTH5130 MBA502 MGT 5380 ARCH 1261 F033800 20LLP109 ELE4009 FINANCIAL COMP3331 Computer ECE4179 20T3 COMP9311 COMP9311 UNSW MFIN6210 ACCT 5930 EE590 ENG2029 ECO100 SIT315 ACCT3610 COMP3600 STK2100 FIT2004 COMP30020 ACTL1101 Stat 101B BANA 200 COSC2473 ENGG1400 AI COMP90043 MMF 1914H PHYS 127 CS584 CIVL2010 ECMT2150 CS 333 CP1406 KIT308 Economics 701 ECON3740 ECE 5759 BFC3340 FINC2012 COMP4500 MATH3871 FIT3080 18-819C Economic ECO202Y5Y PHY100 FINC-780 Econ 100B EC602 IE582 EE450 COMP9517 WRDS 150B ECON 570 LECTURE 2 ECA5101 ECE 4420 ADAD9311 FIT3031 CS 544 MF 703 CS 6140 KIT501 ENGSCI 344 CSC171 IE 332 FINM8007 21S2 COSC 1114 FE545 E471 SIT102 CSC108 MAT301 IAE 101 COP3503 STAT2004 EC 303 CS1026 STAT1203 MATH3171 ISOM5160 IFN657 FIT2014 ACCT2102 DSCI550 STATS 330 ELEC421 COMP3670 QBUS6840 MEES:698B MAST30027 MIET1077 Economics IFT 6758 FIT5122 BUSN5101 CptS 111 HRMT5502 Math2018 PP 312 INFS3200 CZ3005 CSSE1001 SENG 2011 MKTG 553Q BUFN 640 COMP507 ETF5952 DATA 311 ECE4043 BANK3011 finance M3H623544 HW1 INFS 7410 AI6103 STAT3888 INFS3208 ACCT7103 ECOS3013 PSYCH 20B F79MA STAT3006 ENGG952 2X MGSC 7000 ECE4132 MSF 526 MATH 3033 CDS 511 EEEE4120 EEET2465 ECA5103 MATH2070 ELEC3104 BU51019 EEE8147 ENGR20003 COSC 1107 ETF3200 FNCE 435 MSFI 435 ISyE6420 GENG4405 HW ETC5523 IE 7315 MOEC0021 STA 106 ENGG 1300A ENGG 1300 OLET1139 STAT 3503 STAT 206 FEM11149 ELEN 4720 COMP20003 SOLA1070 CS574 C11CS LINB29H3 MAST90083 ECON7200 STAT 610 LINB29 DSM-5 COMP3161 EEEN40010 MATH 4431 K353 STA 3386 IERG4300 COMS W4167 ENG5298 AMME 2302 CS3910 COMPSCI 320 STATS 369 GR5242 COSC 328 CSCI435 MGTS1301 INFS2200 COMP3900 CIS 375 Module AE03 COMP3121 CS260 HAM503 MGMT5050 INT3075 COSC 285 GEOL0029 GEGE2X01 STAT1201 MATH1061 MMF1941H STAT 5060 CS 520 COMP 4320 MSIN0104 000T FINS3648 ECMT2160 ECON4003 Phys 129L CSE 142 CS 3130 MGEB01 EECS 340 Finance (20443/20444) ECMM149 COMP5310 EEEN60180 CSC 111 AT2 CSCI 4430 STAB57 MA/CSC 427 MATH322 D100 CSCI544 CITS3004 CI6227 CSE 565 APCO 1P01 852L1 ELEC S411F COMP3207 STATS330 ECON7530 FIT5149 CSI4104 CMPT 371 COMP201 SEHS4696 FI4003 MATH6182 CG1 WS MATH401 MGT 205 QTM 110 COMP 0137 MACE12201 FIT5210 ECE 544 BISM7206 HUDM 6055 ECON3203 STATS 210 MSCI 570 MATH6173 COMPSCI4039 Accounting COM3503 AOE2024 ECON213 PSYC10004 Control Data 100/200A PHIL2617 PHYS3116 MIE250 BCPM0008 ECN 620 QBUS6830 ECSE-415 ECON5102 MGMT20005 MAT 653 ECO 480 COMP 5/600 CSSE 5600 ME 571 7CCMMS61 CS 550 COMP2865 MATH3075 STATS 506 QTM 220 ISYS2120 FIT5106 STAT 153 MKTG3112 ECON2102 ELE2018 COMP3031 MSIN0010 SCC461 MATH237 CS246 CSC3065 CSE 101 ICTWEB411 COMP9313 ECOS 2025 FN620 MATH11111 MATH 3018 KE1068 FINA 6112 C++ MISM 6202 MSIN0105 CSC8631 MECO6935 COMP4121 ACCT2011 DPBS1150 EEL 3701C F19PL OPM 661 CSE 310 CS918 BIOL30001 ACCT3563 BANK3600 MET CS622 MATH367 ACCT5907 Continuing COMP5048 COMP61021 CS3334 GSOE9210 CSCI-570 COMP 5322 HW 2 ALY-6020 IEOR 4706 DATA 200 EBUS504 CGE12412 COMP4108 7SSMM800 ECMM171P MATE50002 CS225 RS 6003 BH2274 ELEC3111 MAT6669 ECON-UA 227 PHIL 1012 7SSMM603 TB028A P6 ECS708 CSC 427 CS6476 CSE 250A A1A2 ITS61504 EECS 376 model HW6 UV0010 ECON 6074 MG4F7 CMP-7030Y INFO3008 BFIP013 ECON 5068 MATH6002 CS3483 PSTAT 131 C31FM CSOR W4246 AAEC 5307 DATA ELEC362 COMSM0047 ECN6006 MA20224 BST351 MATH 323 MATH323 AA2021 COMP3811 COMP2013 IB9X60 INVP001 EMATM0051 COMP220 BLAW1002 E20 TCP8001 ECON61001 EART40005 ECONM1022 MATH 365 MATH 367 ELEC6218 COMP 5812M EDUC 5061M ELEC ENG 1101 equation MATH6174 ST334 C4 EC9570 A33648 EBUS603 ECON47815 stata WFMS0001 PEM102 INF6060 ionically ELECTRICAL MATH 375 MMW 12 MKTG860 ECON60401 ALY6010 SOST20131 Introduction COM3524 MME2 GGR305 JNB 538 EECS101 COMM5030 IEOR E4601 2B CSC336 EN2315 LAW 432 CSC263 MATH2001 OLET1143 CSCB63 SIT772 COMM1170 STAT 441 MS930 INFT3050 GLBH0030 Stat 120B MAST10007 MGEC61 Machine GGR 252H1S ECON7030 Financial Marketing MGMT30019 ECON5120 SDSC 8009 CSC165H1S DSCI 551 3081W ACM41000 ECA 5304 MATH 1064 ECSE444 DATA 604 COMP7105 MIE1615 ECON4004 ENV200H1S EC481 MKT 306 EC1B1 MATH08051 ALY6140 CS260C CSE30 MSIN0226 CS4103 CSC3064 AM16 COMP11212 CSE4101 PSTAT 174 Math 380W CNT 5106C STAT 310 FIN2028 CS5014 STAT 425 COMP 4102A ELEC2140 MANF9544 QRM 9 QRM 8 ECON 457 COMPSCI 4091 MATH 523 DNSC-4211 PEAS 6000 MSIN0180 COMP2119 A2A HT 2022 IB93F0 MAS316/414 ACCT2522 MSIN0181 ATMS 201 COMP3425 MATH7861 SOLA2060 MA 325 7CCEMCTH ECON 432 INFT2051 SOLA 2060 ECOS2002 Stats141XP BIOA02H3 S2022 MA4601 K5 COMP5329 EG 284 IB3A70 WECO1020 COMP3027 Energy ACS61011 MAST20026 STAT 533 MATA31 ENVS257 BEM2031 EC 486 COMP0172 CS3214 EECE5644 IB2B20 COSC2536 COSC1147 COMP6214 5CCM242A COMP0130 AMME2000 MTMG50: EG238 ACF6006 QBUS2810 COSC2391 ECON7560 MATH377 STA305 CS 486 COMP1117B EL648 ELEC3909 ECON 241 COMP 4901W BUSI4428 ENEN20002 ENGN4524 ELEC3115 CSC 413 PSYC 100B ECON1002 MATH256 ANSC20005 MTHS2008 MATH40082 COSC 2406 FIT3174 STA 238 CMT202 Differential Equations MTHM017 GARCH 101 MATH2069 CSC336S ACSC12 ETF2121 CEME 2001 DB B474F ARHT1001 EECS 3311 3220 STATS 786 CS 484 COMP20008 MATH4091 ECE 455 CSCI 204 BUS B200F BA 875 BU5562 COSC 1147 X11 GEOG 101 IMM250F CSE 584A MATH38172 LAB 4 ELEC5882M FINS5523 EE 430 COMP 465 6CCS3PRE 7CCSMNSE FINANCE ACMB02H3 ENGG2112 ELEC5616 SCM B371 CHEM3120 CS22 ECMT2130 MAST30011 ADSPBF706 CENG0013 ACCOUNTING BUSS1040 CHEM 181 MAT136H1 GY 6183 COMP3170 AGRI90089 PHYSICS 1002 ECON10003 IEOR E4004 ACS61012 MATH 40550 MKTG2113 TELE4653 ENSC1004 ECE 232E MK726 MTRX2700 SHEET 3 CSCA08 COMP30027 Math 2XX3 statistic MMAN3200 BISM7213 ECMM109 ECON 2022 FNCE 20005 GR5067 CSCB09 ME 3017 CS 5100 PHYS 2903 COMS 4771 COMP222 COMP 1046 CSC148H1 ISYS2038 FINS2615 OT5206 COMP2048 A6 MECH5770M MA826/20 CMPT 726 STA457 INFS6071 INFS588 integral ECON 216 IRDR 0017 MA323 PA 15213 PSYC2001 ENV222 Statistics ACCT5930 ACCT12 LAND2121 ME 5405 COMM1180 TELE3113 A7 ECE 568 ACCT2019 INFS1200 ENGG1340 CS 1400 ASST3 FINM7409 SWEN30006 INFO2222 FIN20150 SOSS1000 CSSE7231 FINS5513 COMS3200 CECN 702 ECON4060H MN3515 HW2 PSYA02H3 ECON 2112 COMP90051 CS 1652 MA30059 AF1605 MKTG7501 ECO-6003B COM4521 CTM ECON3350 COMP 3804 ELEC9762 BISM 7255 ST22 MATH20014 MNE3122 COMP343 MATH5165 ELE7029 ENGR30002 SEEM3500 ECON7350 RISK5002 FINM7405 COMP90059 MOS 3320B STAT 431 BISM7221 MATH3014 MTH783P EBA 35302 ACS133 BUS2206 IE5600 ECOS 3997 EDST2003 FIN 534 Elec4430 MATS3001 MGT6047 FINS5514 MIS602 ATS1279 ECMM445 2F CS262 EFIMM0097 FINM2002 ECMT3150 FINC5090 WACC1000 MECH4620 ECOS 2002 SEESGS79 STAT COMP3007 BUSB200F ACST8040 CAES9920 STAT0020 INFR11205 PHYS2111 FINM7402 STAT 428 SOFT3202 ME220 ACC-ACF2100 EC9410 CSE 120 COMP90042 SEE5211 ECON0048 BUSN2036 MKT2010 3SMFE4 EFIMM0117 ECON3034 MTH5120 EFIMM0120 X0 W19186 MATH 034 COMP2100 COMS4104 CS1210 MENG10005 ACCT 5906 ECMT1020 MGTS7607 MATH3090 CIV4100 CSYS5020 ELE2019 PHS4200 ACS6124 MSIN0225 PHAS0061 6CCS3BIM FINM7403 COMP8410 PY406 COMP2620 CS226 SDEV2004 COMP6080 BFF1001 HR410 MCEN30017 AMS3328 ML3 ELE8059 FINC3017 ACAD001 FTEC2101 ES480 3D ELECTENG 734 MTH731U MATH-UA 251 CSCI-UA 9473 A2 MSDM5058 FIT5047 COM6012 1FIN B386F MPHY202P ACCT6003 ECE 6913 HMB312H1 AC1025 MTH6105 Math6168 FINM 3003 CS24320 PHYS2134 ACCT3011 MECH1400 COMP30024 ENGGEN 121 COMP3721 MCD2080 ECON 7002 MAS439 COMP6216 ECON2011 M23367 CSC597 COMP6247 BRIEF QBUS6180 EENG22000 FN1024 MATH0094 MANG 6554 ECOS3003 ELEC6252 C2511C PHY328 EC1060 ECON32202 COMP4002-E1 MATH3063 EFIMM0124 QBUS2310 ECON4411 FUNDAMENTALS ACCT20001 18YX RPM COMP 2711 QBUS6600 BUSS5221 ST3189 FIT1047 MAT344 EGB375 MATH60013 MATH96011 COMP3557 MAST20029 ECM159 EAE1011 ENSCEN 105 SECTION A STA 141C SOSE 2022 PAM006 COMP0048 M40007 ISOM2500 CMPE 142 A06472 MCC150 ACST 8083 GEOG6087 ECON920 FINM7008 ENVENG 4110 COMPSCI 361 ENGRCEE 21 PHYS 1112 ACF2100 ECMM108 COMPS267F MAT00050M MAST30025 CSIT970 MSCI 224 INT202 PUBL0054 MSDM5004 BMAN 21020 BMAN21020 MGMT1002 MATH11150 LAWS7023 ACTL30002 CIVL3340 MATH1002 ECON 8069 COMPSCI 351 IBUS7302 STAT4528 CHEM1101 STAT3925 BUSN 7008 Comp 3120 ECOS2040 SWEN90010 ENGN6528 ECM158 ECON20022 COMP6452 Calculation CITS1401 S1889112 BUS 351 ACTL30008 FIT2091 ECON6002 IBUS6020 PHI 001 ECON30290 MATH7501 ECON10004 MFIN7017 ISYS90043 LAWS7012 ECON30025 COMP30023 COMM1190 ECOM20001 GSBS6009 STAT 337 EMET8002 ECOM90001 ECOM30001 FINC 2012 BUSINESS ENGCV512 ECO 101H1 IB9520 FINM 3008 ECON7310 FIT 1006 MANAGEMENT MATH3821 MTHM504 CS975 COMM1100 ELEC2133 MMAI 5500 MIS611 ELEC3114 CS 173 ELEC 3105 ISO 9001 IDSC10 Rural livelihoods and globalisati IDSC10 K17 202 CS823 MAST90007 SPG8024 MAT246 EG-264 CVEN2303 INFS1603 3PR3 MN-2508 4CCE1MCP SPG8030 CMT224 Inflation consumption Applying MAT137 CSE 111 DPBS1110 FINS5530 ELEC4613 GSBS6200 COMP4336 Math W54 DIFFERENTIAL 7PAVMALM ACC 1110 ME 3210 MATH2801 MGMT20001 ECON 6202 PSTAT 120B COMP9024 ENG5027 comp3219 ELE00107M ECON20003 ECON2103 FINA2209 MAST20018 LUBS5308M01 MATH2023 Computation COMP1600 CHEM 3X23 BBMM506 FNCE20003 BMET2922 BISM7216 financial ECMT5001 ACST3059 MAST30012 COMP3511 ECOS 2201 MKTG7512 ECON2540 MTH1010 MAT1841 COMP4600 ECON7740 PAPER C331 CAP 6617 ECON2420 ACCT7107 HLTH 7001 ECOS3002 CVEN30010 MAST30021 MATH1014 BIOL1007 ECOS 3010 SWEN90016 BISM7202 ACCT90012 INFO3315 DSCI 553 INFO90002 COMP3419 CITS 3001 EE5731 FINA3326 NFS 284 COMM2501 FIT2104 PHYS3035 RSM260 MAN3080 CHEM30028 MATH2088 ELEC0144 MECM10006 2D AE 202 ENG5022 CHEM3121 FINM7006 CS5340 CSE 594 FIT9136 FINS3633 RSM222 STAT3017 CS 8395 MAST10005 AMA546 ETC2410 FINM 7406 MSBA 7004 BUSS6002 CHEN 90038 PSYC20007 ACTL 3162 DIGITAL COSC 2670 PROGRAMMING ECON 5007 FNCE90045 PSTAT 126 MATH2307 STAT7055 SOC 360 BINF2010 WSTA01 AMME2200 ECO 204 BIO773P BU 312 AERO2598 ENGG 5103 ECON1010 ECON3031 MATH3078 HPS319H1 COMP26020 COMP42215 ACCT7106 COMP3271 MKTG10001 ECOS2025 MATH36031 CSE 402 ACCT1110 ECON 20005 MTH319 COMP 3711 PHYS1160 COMP3601 MSIN0026 ECON1202 ARCL0103 PHYS5033 PSYC 171 QBUS1040 ATOC10001 1ENVS222 COMP9032 CIVL2812 JURD7152 CS 449 ECON 7073 INFS6015 INFS7203 MATH2521 ECON7073 CSE101 COMP2121A DSC 40A MGT3009 COMP4161 FINM8006 BUSM054 COM6503 ST443 P 500 DPBS1190 ELEC5101 STA457H1 MATH3411 COMP5216 PLAN30081 STAT7203 MTHS3003 37T37T BLAW30002 GY7702 MATH580 ME 3057 PHYS 2012 ACCT13 ECON 3210 EE7207 ECOS3005 EC 502 MATH1004 CC0675 PHYS 4315 FINS 3636 COMP1012 economy ISE 562 MACS 30121 ML4ENG ECOS2201 ECOS3008 ECON312 PPGA 503 COMP26120 COMP2511 COM00111M CMPU4021 HP435 ELEC1111 ACS61013 MAE 8 ECOS3007 ENGG5103 FINS5568 PHYS40001 CS 0002 IB9W00 CSCI 141 ACCT5942 FINC6015 CSCI 3150 ELEC1200 CSC236 CSC236H5 CIT 593 CSCI3170 ACCT5908 CCIT4076 COMM5011 MGEB11H3 MGEB11 MATH42715 CSC236H5F ELEC1703 CS4203 MGTS 7603 MANG6529 MUSI08076 EGA366 EIE4432 1EECS 261A CS-521 FIN 708 MN50374 MSBA7027 STA 4373 MGEB06 PHYS4291 Model HW 3 MCIT 593 MSBA7021 CS5010 ST326 COMP0043 ECON-371 ENGF0004 INFS1602 MAT6679 ECON1020 STAT40830 CSGY 6923 CS280 Stat GR5204 CIV6115 POLS0012 ACS6127 MKTG1001 MTH305 CRICOS 00099F SBSD 2063 BE332 ELEC3201W1 EC320 SOC100 COMP 1405 ST 311 COMP 4337 COMP4337 ECE 380 MATH1013 EENG35010 IHSS1200 CSCI1200 ECS 189A ECON4010 ECE 368 EGA324 SCC462 ECTB61 COMPSCI 589 N2 COMM1120 STA 313 ELEC 301 COMM3030 ECE368 ECO204 ECOS3020 MAT 246 STAT4620 GSOE9820 CCT110 MGTS7303 ACCT11 STAT3010 FIN6108 EE 6225 STAT 3450 BUSS2000 STAT0024 CSC 240 COMP6741 MATH5975 CMT316 ISE 535 210FIN316 MGMT10002 COMP0050 EC306 FIT 5124 59PM ET S2098367 CAD MMGT6001 COVID-19 COMP5940M ARC181H1S SCC 312 ECO102 MATH4061 ELEC 3848 DATA3888 MECH0024 STA302H1 CSE 510 LAWS8214 WORK6108 E2 ECON 7310 COMP3211 FIT5216 A4 MATH 110 IBUS 1101 CS355 SWEN90004 MATH1023 BEEM012 COMP3311 ACCT90013 EES A06 EC 504 ISE 580 ENG4701 CAS CS538 ELE3040 6013B0506Y BENV0115 ECON3104 CSCI-1200 COMP27112 IEOR4703 ELEC271 ECE-GY Math 412 BUSS1000 PP208 BCPM000028 7QQMM316 BISM7209 DASC7606 HW 4 STAT 4620 ECON8026 INFS3202 COMMGMT 3506 COMU1002 ECON 20003 MATH 348 BUSN7008 BENV0113 STATISTICS Function STAT2001 ECE6483 MATH1115 MGMT20002 CONSUMPTION ECO00003I LAWS6997 APMA 4300 ECON 7030 STAT 413 802G5 GEOG0051 LINA02 ECON 3208 GOVT 1621 ECOS2001 ECON 7520 MGTS7301 ECMT 6002 MATH4321 EIBS7300 MARK5813 BH50A0220 OFFICE280 ECON1012 CIS273 CIS 273 ELEC3106 ACCT3013 EC831 MMAN3400 EC365 MAST20006 ECON7520 ENGM030 CSC148H1S COMP5125M CMPSC 497 ST5188 MAST 90082 CSSE3010 ECON7040 GEOM3000 GEOM30009 ACCT5910 ECON7001 CPEN400D AMME3500 IDSB07H3 Management BUSN7050 ECON1003 7QQMM312 CIT 5930 MARK2012 ECE 466 STA 365 MIE1621 IB98A0 COMP3278 PHYS3888 BUSN7036 GEOS2121 MATH 368 ECON2020 COMP2111 ECON7110 MATH260 INMT5518 PM 410 mktg3110 econ6021 ACCT867 CS4182 PP 202 COMM5000 ECON1101 ACCT90030 MAST30013 00025B FINM2416 ECON7300 FINC6001 SOST30012 ASTR1001 ELEC 4510 COMP5206 POL200Y1 PSYM204 EMET1001 MARK5820 Math 9B ECON7070 PSYC3001 COMP2212 ST117 ECOS3997 BISM7255 MSIN0068 MAST90045 MCD6110 ELEC 5516 MANG 6563 AIML427 CS3402 PHYS3152 PHYS 3152 AMME2500 PSYCH 727 CHAPTER 6 DATA7201 FNCE90062 COMP9003 COMP0137 5QQMN534 COMP1730 DS 2023 FIN3016 COMM5007 ME3255-001\ ME3255-001 COMP0025 ACCT7101 CIVE5001 MEMS 424 Stat 133 DECO2200 GEOG0005 Module 4 ELEC2540 CS5011 ETC2440 PADM-GP 2902 MATH 0050 BS3326 INFS5730 W9 ECON 3440 MTHM606 SECU0057 FINA2322 FINM7407 STAT1008 SIEN6006 Economy RME30002 Correlation ACCT2511 ACCT 2511 SSE2 COMP5313 SRE302 ECON42115 ECMT1010 5QQMN533 CS-677 COMP4038 INFS5700 IDP2 MACC7012 ECOM 2001 ECON6015 MATH2115 COM6015 ECON30020 EMET8005 ELEC 7313 MGMT2017 BEX 5601 SOCI10001 MAST10006 Calculus MAST10006 STAT 3022 STAT3022 BUAD 203 ECMT3110 CPT206 STATS 782 ISM7206 COSC1076 BEAM038 Applications ISYS90049 ECON 7110 FINC3023 FIT3182 MATH1015 ECON3440 ECON2800 reinforced PHYSICS MEC3010 BMAN60422 AMB201 EC326 PHL100 FLTV10010 IDS 136 stat2008 ECON6008 MKTG6010 ECON8069 3000K MGTM14 EC201 BUSI97064 BFC3170 S1544 ECON30006 COSC2002 CRICOS00099F MATH1005 COSC2759 MATH 645 EC226 ECON7021 MAT 3375 CSSE2002 ACCT5919 POLI 100-921 MGMT 5050 FILM1000 Math 142B MARK205 ACCT 90002 BISM3205 SA 101-4 COMMGMT MTH5210 ACCT2542 ECON3106 SOF203 ECON3107 INFS3603 INFS5720 MMAN2300 FINS 3626 ECON1102 TERM2023 COMP9312 ACTL 1101 SCIF1004 INFS5710 IB9QR0 COE 0449 TABL5543 CS957 COMP9444 ECON5101 ECON2101 FINS3637 qbus3330 MATH1021 ICOM6034 MAS2011 COMP9021 MA280 BLDG2220 DATA9001 CSCB58 FINS5537 SCEE08003 STAT 131 CS-1520 COSC3500 MEC2007 MTH5520 BSB108 DPBS1140 CMT304 MTH6155 GSOE9340 MATH226 BUSANA-7003 MGMT2016 MAST30034 mast30027 CENG0011 FINS5510 FAQ 2023 ECF2721 COMP3610 MCD2070 ES2C7 Biochemistry CMT107 MTH5510 MATH3301 CCC ENGG3112 NSW2226 MUF0062 COMP6390 Econ 7322 IDEC 8022 MGTS7610 FINM2001 PMGT3857 ICC104 FINM7007 2A ETM5900 MATH0028 COMP0080 CHEM1012 MCD1560 MATH3061 ISYS90112 FINM2415 PSYM201 BADP2005 CHIN20021 FINM 7402 CIT 5950 AMME4710 FINM 7409 CIT 596 ACX3900 COMP30026 ACTL30004 STAT 3058 Functions ART MAE 4341 ACCT2110 STRALIA 83 ECOS3029 HSBH1013 FINM 3005 INFS4203 FIT9137 ELEC1601 PHYS 420 MATH4512 MAST20005 QBUS3600 FIT2902 ISOM5230 ACCT1101 math40 PSYC2017 EFB210 PHIL2467 CYB102 MKTG3501 COMP9900 COMP4318 ​ECON7310 COMP9201 FINA5525 WRIT1001 FNCE90016 PHYS420 ACT0200 CLO2 MAST10010 PSYC30019 OB0224 FIT3172 ACCT5906 ACCT6001 MATH 317 COMP4418 COMP90049 NPV 283 MKTG7505 FIT9123 FINM3405 MKTG2004 MIE 360 MAT315H1 FIT3138 STAT 6058 BCH210H MARK5816 IBUS6002 COMP5328 UDK621 CEN311 COMP3301 CCB302 BIOL10010 FIT2092 ECONS3013 FMAT3888 FINM7401 EDUC 263 MECHENG 715 UA 132 006 MFE 2 MAST30026 MULT20015 ECON7950 COMM5010 CITS2211 AERO 3465 ECON20005 GR5010 SCDM71-316 PHYS4050 COMM1140 ACCT5996 FINC6013 ATS2946 FINC3012 FIT9132 COMP9418 COMP90086 STAT3023 MATH3975 ECON7360 CAVA1001 ECONOMETRICS STAT8003 ECON 2050 CCB303 MATH 242 SIEN5001 CSSE2010 FINS5542 GEOS 1002 ECON90015 MECH4900 GSOE9011 MGTS7621 ECON3123 COMP2501 GEOS 2111 ACCT 5972 MDSB03H3 Medicare math4512 MGTA01H3 CSE 3341 STEP INFS7410 CS 335 ADVT7506 MLP 2023 ELEC9711 MECH9761 FIT5206 EL9343 BAFI1002 INFS7007 ECOS3021 SFWRTECH 4SA3 COMM1150 EDGU1003 CEN207 ECON2111 3FH3 FINM3407 EVT802 ECON2560 Credit Cards Operations COMP 9517 CSC71001 CAB340 2701ICT CS4417 CSC 226 EE 559 Application scene CSE 482 COMP 1406A CE315 COM S 228 CSE-141 functions EE 634 CS 450 COSC2675 CS 2c03 CS-350 The main principals of the algorithm CS 369 COMP1406 FIT5212 cs5200 Comp2411 ECE-GY 6183 CIS2344 regression COMP 418 Business MDSB61 MGMT3001 BE334 ECN115A MARK5811 IS524 1INF 1344H MECH0023 MFIN 705 COMP7015 FINS2618 PHYS1110 CE150 MEC3027 MGEB12 BSBOPS601 HCD206 COMSC 260 ISSN 1913-6005 STAT 4261 MKTG100 ACFI310 MECH0026 MSIN0096 OPTI 570 MATH253 ECON2040 0CE163 CE163 CS 580 ECO579 MA407 CSCI 2500 PHYS5140 BUSM1026 CSCI 1933 EEE335 CE142 MATH363 Earnings CSE 103 ACC7011 MATH-GA.2901 ECON7002 BE3336 BEAM046 ECON0027 MCD6020 GEOL0016 MAT 319 6QQMN562 ST305 ATS1248 CEN331 BU527 COMP0015 PSY320H1 HPS370 1MAT 246 EENG 34050 CS3342 MH4501 APM236 MARK5814 MGMT5601 ECON 323 B31SE SWEN20003 MAT301H1 DTSC301 GNSS COMP37212 POLS0043 APM462 CE164 ECE-GY 6113 STA303H1 PGBM161 GEOG7128 AC 420 COMP4920 ENGG 5402 MATH-UA 250 ELEC-4840 BE630 ISBN9780 BENG0019 DPST1091 ISE529 FRST30001 MIE245 PSY220 CVEN4503 ACCT 90013 COSC3000 ECON5069 ECON2070 MMGT6016 code METR4201 MIE 1624 ECC2000 ECON 5248 COMP9321 DECO1100 COSC2527 SP24 MGMT 90015 ISYS90076 MATH2320/6110 INF 2179 ELEC3285 BMB6001M MATH1062 ECON6300 MGAB03H3 STAT2032 COMP226 FINM3404 MARK 5800 COMP1100 PGEE11136 COMP3221 ECON2206 POLS3104 ENGR527 FINS3650 LLM ELEC9731 BUS 1300 MDSB25H3 GEOL0017 OLET1403 COMP2400 LP ISYS90039 COMP 2121C ECON 2024 MUS303H1 CS 443 ECON-UA 323 SEEM 3580 TABL 5551 COMM1110 GSOE9510 CSCI 4210 1MKTG 90004 ELEC4614 ACCT5931 TABL5551 MATH2010 MATH3121 ACTL 2131 MATH3426 MIE363H1 MKTG3506 MATLAB MDIA 1004 INFS1001 CIVL4903 ELEC9713 KKB180 IEOR 156 BANASD604 SRAP5001 EE2023 MATH 3640 MGMT2001 FINM4106 GSOE9010 BFF3841 PSYC30014 matlab ISSN 1816 LAWS6810 LAWS8213 ECOS3006 BEX 3000 FINM7406 MATLAB02 LAN ACCT1102 974N1 TOUR1000 COMP3015 BMB6007M COMP3310 FIT5145 EFN344 ELEC373 PRINCE2 FINC6010 GEOL0073 MATH404 FINC5001 STAT 3303 ECON5004 COMP2006 ChatGPT LAW40615 ACCT90002 MGT380 MUSIC MTH161 ACX 5903 MATH-UA 132 ELEC3004 ISSN 2320 BOEING 737 FIT1093 econmice LAW46315 QBUS6820 MATH5340 STAT3922 SEM212 MATH2061 CCT 109 CCT109H5F MGMT90141 COMP4403 Compiling DATA7202 CVEN30008 COMU7311 FINM3045 QBUS6850 SO44CH19 ENVS10001 INFO500 FIT3175 INFO90004 MKF2121 COSC 1285 COMP2750 ESSMENT 2 MM1MS1 ECON 7430 ENGR10004 FMHU2000 STAT8130 ECON2060 BSAN2204 CSSE7030 FMHU5002 PHIL2623 ECON7150 MTH3320 MMME1043-E1 MKTG 3110 FIT1006 MATHS 328 MKTG7502 ECON3116 ECON5106 COMP9727 ROBOT ACCT5961 ACCT5459 MKT3SMK MGT807 Variables art Consumer EC7103 COMP2041 PHYS 210 Algorithm COMPSCI 210 CMPS 101 COMP 451 CSC 230 COMP 8042 CMDA 3634 EECS 132 CSC1001 SCIE1000 FIT9131 ENGR2881 ICS 45C MPCS 52030 CMPUT 201 CSE3321 CSCI3120 CPSC 351 ENSC 251 CPT109 ai program FIT5037 UNIX EECS2011A STATS 730 ETF5912 CDA 5106 MCG5138 ICSI 404 COEN 346 MPP Inf2C MANE 4280 CMPT 454 M226 -1 CSI 202 COMP0017 CS33 CS 211 COMP2401 MATH5350M CS2035 CS 464 Matlab CS 280 COMP2113 CptS 122 BIM 252 CSE-111 CSI3131 ECE 449 ENGD3104 Algorithms 3027 ELEC6228 CMPEN 431 CA2 COMP-3300 ENGN 6528 COMP2011 AMATH 301 3340b CSE130 CSCI0201 CSEE W3827 SIT744 EEE3457 CMPSC431W MA 3502 CSE 332S SCI 46 BUSA8001 ECM3420 CSDS 325 Computing MA3602 32516 CSCE 411 COMP2221 openMP CSC252 W4111 PSYA02 COMP9511 MARK2085 cs3121 LCOMP3121 COMP1046 ECE6443 Modern COMP2932 CSC 305 COMP 202 SYSC 3020 CSc 360 ECE220 6003CEM CPSC 326 CS202 App CMPSC311 ECO 521 INTE2401 COMP2300 CSC246 CSCE 421 IB9150 LA90 COIS-3380 CS 6823 CSE 40431 The Class Concept computer vision due CISC181 Development OpenGL FIT5196 CSCI 3171 COMP 1039 CP5633 COMP 3007 COMP 31 CS157B ECE 434 Engineering 265 CSE 3461 EECS 2011 COSC1284 CSCI 4470 CSE 582 COMP331 CSC 311 SCIENCE 1027B 7088CEM COMP2150 COMP3760 SENG1110 COMS 4771-2 COMP3620 COMP 2019 CS 313 CS 3500 MATH7232 MSCA 31013 CYBR 150 Art c++ COMP1110 CS 540 CSCI 3302 business computes ECE498AC COMP 9020 Master CSci 5521 ICT30005 CS 5800 cpts350 ICTWEB510 ISYS1055 CSI213 OSC 2111 CSC242 JavaScript Comp6310 CSC311 cs4417 CSCI 5525 ITEC 2610 COMPUTER COMP90048 Com S 228 CS218 COMP9322 CM20256 CIT325 STAT346 COMPILERS W4112 CUS 1185 CS261 COSC2413 CEGE0096 java F19 17601 SCC.413 CP2404 CP3404 CS6262 CAB201 CSE 6242 SIT764 CMPT 291 CMPT 365 CSI 508 CSCI 103L CP2403 CS214 ACSE CS699 FIT5195 Analysis CS 570 CS675 CSCI 6140 SENG265 M3C SE 3314B INF60009 SSMM603 INTE1070 STAT 380 ISYS1101 Robot CSC 373 PROG2007 HS1031 MIS 380N MECEE 4602 CSE2DBF ATM 149 COMP 352 COMP SCI 7094 CSDS 310 CS213 programming MAT022 CSCI-GA 2590 CS124 CS5281 SCC300 CPSC 4910 COSC1111 coding UTS 41225 CSI 2120 Comp580 COMP SCI7413 statistical Research Proposal COSC 3P71 Sudoku CS 3600 3806ICT COMP 1020 ​CSCI 4430 Processing COMP SCI 2201 CIT 594 ECE-171 Analyst ECE 46300 CMPSC442 CPSC 5360 COMPSCI 313 COMP522 Mathematics 3159A CDS504 CMP-7025A Data FIT1050 DSA1002 SIT323 CW1 CS300 Maximum INFT 1020 Econ 318 Systems Modularity CS146 ECE463 CSCC01 CSE2ICE SYSC 4602 Pstat 160B CP3406 COMP 596 KIT102 SIT742 CP3403 ECE 4/574 CS 542 CS 338 COEN 280 CMT311 COSC 1073 SSCI 581 ECE 4/574 Homework ECS784P CS 326 CS170 CS2CO16 COMP 2402 CSC 485H CS6083 COMP90041 COMS 4701 CMPT 456 COMP10062 LE/EECS 3421 Com S 311 Comp2300 Algorithms ISyE 6202 SD6501 B9339 CSE573 COMPX554 CS 4417 ITNPBD7 ICO155 300693 WT CS 577 CSCI-561 IDEA9103 COSC2758 COMP810 database ICS3U1 COIT13234 MATH2501 MGMT5800 ECE 103 CSCI 620 ITEC 3220 CMPSC 448 CSC458 CSC209H COMP 3004B Value BT2102 CSE 347 CS434 SIT202 CS 179 ICTPRG528 MPHY0021 CSE4DBF COMPSCI 230B CS318 CSCI-311 CS6310 Math381 CS 5710 6CCS3AIN CSSE7610 CSE 141 CS 61BL application COMP1350 algorithm CES 422 CSC210 System INFO911 SYSC 3310 ALY6040 CSE 12 PA2 ALGORITHMS COMP2042 CS112 CS178 Web CS 535 ELEC3270 NWEN303 SD6503 CSCI127A CS 352 STA 4202 Comp2123 SIT720 7CCP4479 SEG2105 CMT115 CSE 260M CS 6212 COMP 303 ENGSCI 233 COSC 2391 CSE 240 COMP9103 CPS 3500 CMPEN 331 ISYS 1117 CMT120 CS 435 COMP3258 cs9024cgi COMP0012 CSCI2110 COMP5046 ITS63304 COMP503 CMT 202 cmpt310 CST8218 BUS 440 Database COMP 1010 CPSC 231 COIS 4050H Engineer 2813ICT CSI2120 CSSE3100 CSE2/4DBF 301110 CS1027 CMPSC122 MAST90125 COMP5416 CEGE0101 COMP 3704 COMP4620 COMP8711 EECS 461 CMSC 421 COMP SCI 3004 EIE3373 CSC3150 MP2 DECO2500 CS1315 CE243 CS 341 CPT205 Cmput 455 ITECH3107 CMSC 420 CSCI262 SCC.311 COMP8101 IAB320 CHC5028 TSP ICC565 CS512 320SC COMP2396 COMP207 SVM BSCH EECS 2101 COMP3230 CEG3136 INFO 3440 EE3009 MGT7174 COMP 3334 ECON20120 Econ 702 CFRM 505 CS4001 CSE 328 AMATH 482 ENG2008 MATH39522 DTS101TC CSC318 EDUC 124 NBA 5110 ECON0125 ELEC7310 EEP101 ECE 777AE MDS 6112 Bioc0036 ACCFIN5246 STA 404 CFRM505 Chinese 2241G MATH 376 AUENV 218 ELEC0006 ACCT 3230 FIN3020 ENVM3115 CMPSC 464 EE 4233 CST 8284 ENGI 2211 EEB240 COMP52715 PHYS1120 ECON0019 MAT187 FINN1037 CSci 5421 7SSMM803 STAT 400 LUBS5996M ELC5216 STATS 4A03 ENGG1003 BADM 3661 DATA423 ST332 ECO2121 6406ELE IB3K20 CSE 465 CSE115 CMPUT 206 ecs150 INU1111 QM222 DTS204TC MATH2319 CPT108 SENG6110 MATH3041 INFS3604 MA 4704 CIVIL 750 EEEE4123 CS 3800 comp3511 MEC206 CSCI-UA.202 IOM 302 NBS8295 BMS 201 ECON 3018 ESE 605 ADM3225 STAT7038 Economics 409 ECON 503 MSE800 4SSMN902 IEOR E4106 FRE6831 ISE 563 MATH 451 ECON0001 COMPSCI369 CITS4402 MA1608 MQBS1030 MUSC1982 CITS4012 ACC202 BAFI1026 MA117 ECON5074 MN-3507 ECON-UA 11 AC3059 FIT3094 STATISTICS 260 EC333 MUSIC 2F03 BPLN0025 Math 632 ACCT40115 EC3044 EGEC 540 MATH 521 MATH 131B Math 164 PHILO225 ACST2001 CSI2108 ECE 5041 MSINM014 ECON60822 MATH350 EPPD1063 ECE 3561 STATS 101 MATH2014 ECON207 WEBSITE EEC180 ACCT2343 COMP24112 MATH21112 STAT141B ECON7230 CCT109 H5F COSC2531 MGT 180 ECO 2173 CSE 30 ELEC9714 DPBS1120 ​SMM069 MVP CV4 7AL SDOF SYSTEMS Architecture SQL DS1000B STAT 3701 STA 442 GU4206 ECON 331 CSCI 3120 STAT600 ANLY-511 STAT2402 CSE 2011 GR4206 Stats 20 SCIE4401 STAT464 CSE 230 Network Econ 3818 SE-555 Applied CSCI3180 FIT5197 Robotics 41013 CO004 CS 200 MANF9472 CITS1001 CSE 320 COMPSCI 335 CSCI 3022 OPIM 3220 CSE278 ADM3308 STAT 467 STATS 731 CMSC 216 Mathematical PHYS 454 MAST 333 CSE20W21 MATH2302 MF 796 CS 2100 Mathematics Math 3FF3 CVEN2002 MATH-UA.0252 COMP344 CS631T KNE488 ETF2700 CS314 EGB242 ECE 2671 AMAT 592 MAT 581 COMP1037 ECO £404 ECE-5200 Maths CSC570 COMP284 CSCI3287 EER CS BDT5002 FIT9130 COP4600 CS348 CHI2550 BIA-656 Comp 271 CSCD43 SQL code INF 559 COMP5434 MAE384 Stat 384 Microeconomics Econ G25T Econ 331 STAT 252 ACFI3422 STA 104 ECON 4261 Statistics 305a ECMT 674 Markets Statistics 506 Statistics 4205 ECO6133 ECON 327 Stat 525 Econ 107 Trade 178 Financ CGE13111 ECON 308 MANM301 FIN 450 INVESTMENTS STA355H1S Economics 454 Networking STAT375 IC205 ECON 4850 MSCI 523 NN5-096 BMAN 20821 STAT0029 FM50 ACCT 374 Digital stock MgtF 405 COMP0040 STA414 BUS10306 Comparison CGE25111 EF 5070 GGR321 EC471 EF4321 Econ 101 ECO 404 ANLY550 CMP2092M CSC8111 CSCI 520 Shooter COP5612 FINA 6421 CSC8001 CSCE 101 Software EECS 12 CS2105 COMP 204 EECE 5642 Final ISTA 131 STAT 7008 CSE 468 MATH1058 CSCI3104 COSC1073 CS 112 CSC 1011 CSE105 JSP CP1802 ACS CS2230 CO2017 EECS 233 CSC 656 INFS1609 CPS 350 EBU5502 AACS2204 CO7506 TCSS305 CPS 209 CSC 220 CSE 216 CM3114 CSE 17 CS2C CSE3320 ICT162 COMP 348 EECE 2160 CS 381 CS 3305A CIS 657 CMP2090M CSCI251 IY3840 CSCI-UA.0480-11 COMP604 DSA 5005 COSC 3319 CSE 270M CIS 3207 Programs CSCI 2132 CS270 CSE-381 COMP3230A CIS 212 CSI 333 FINM 326 FINM-36702 Introduction to Software Analysis EEE102 GNG1106 ECS 60 CS 161 CSCI851 CSE1222 EDPS0249 TCHR5003 ANTA02 BBUS1SBY SOSC 1140 MDIA2091 FINS3641 INSY 661 ITEC3040 CPSC 481 computer DEE3519 COMP304 CSE536 Microtheory OFFICE 280 CIVE50003 COSC2673 ECS784U CMPSC/MATH 455 AMA 505 CSE 158 BUS1040 FIT3179 FIT5202 Math 104A Math 111A MBUS107 COMPSCI 761 COMP3710 COMPSCI 316 COMP559 COMP557 CP1 1902 COMP 310 ECED 3403 COMPX523 AGCM 3103 EMET 7001 ENGR3821 CISC 124 IPC comp20005 CS 323 CS105 STAT 326 MATH4007 CS4551 COMP1000 ACIT 4640 ENVX3002 CS2034 FC712 algorithms CSCI 4155 CSI4142 POL 850 MATH20811 2B03 CSCI803 Economies COMP 2016 Architect TRADE INFO1110 FIT1043 networks Robotics ICS 31 ECEC-301 FIT2099 CS 3640 CSE1010 Computational COMP1001 CSE 231 CS10 FIT5166 CSE 400 CSCI561 Math 350 CO-496 ENGG6400 CSCI 1133 COMP3055 MATH 819 CSE 6363 CIS 555 CS4420 COMP0037 ECS 140A Spanning Tree Protocol network Statistics 100B CMPSCI 383 CS 659 CSC 120 COMP 74 CSCV 460 CSCI 2121 ENG3047 CSE 491 PHAS0020 MATH 185 MSCI 517 CS201 CSE 220 COMP 527 CS602 MTH 496 CS909 CS 116 AMS 315 H64RFL/P MGTS3603 ARTS3463 FIT1045 PL241 EE5434 Coding MSF 503 COMP255 SEC204 GNBF5010 JIT104 ECE241 CS 545 COM4509 STA 3187W ECO-5006A DS 310 CSE205 IB9Y8 CSE 3100 4COSC001W IN1900 MGT 201 CSCI 1100 MAT2040 CMPT310 CIT 592 COMPSCI 753 CS 231 CSc 110 MET CS-677 COMP0027 COMP 5416 CPSC5610 COMP7104 SIT215 CSCI 4146 EE6435 CSc361 MSBA7003 CISC 360 COMP3020J CS 320 COMP101 CIS667 CAN201 6CCE3CHD COMP3008J C200 DAT 500S EMAT10007 ST309 CSci 1100 DSC 20 CSCE 474 INFS2044 COMPSCI 711 PROG2111 COMP2211 INFO6002 COMP524 ELEC 9741 IN3043 CSCI 1300 CS101 CSI2110 ITP4514 ISIT312 MATH1090 MATH2019 DS-UA 202 CS 166 CS265 ECON-100-001 CSOR 4231 ECS759P COMP24011 CS 8803 CS 453 INFO90001 ARTS1240 ECN340 T2187 ECE 522 COMPSCI 367 S6140 MA9070 CSCI567 STAT535 MATH 1021 CS 33400 6006CEM MIS501 CSE514 MATH35062 ECON6101 CP1401 PSY4219 COMP304-23A FIT5222 DSCI-553 SYS5020 INFO 5304 ECON0024 OMP9727 CSC8636 MATH60026 6CCS3ML1 CS5012 AIC2100 CPSC 217 G1109 2XC3 CSE 470 COMP2051 EG25H4 CS 7280 CSC1002 Stochastic CITS5508 CS 2820 IERG 4080 SEHS4515 CSE8313 CPS 400 CSE 3521 CIS 313 IS2150 COMP41620 LP002 KXO205 COM6471 COMP 2140 CS251 ITE3101 CST205 CS 340 CISC124 ECON 128 sCSCI3310 COMP0004 MLE 3 IT114107 CSE-3342 LTC2946 COMP122 CSIS 1119B CS560 CS210 COMP2050 CSCI 340 STT481 Econometrics ECE 6100 PSTAT 170 CS5003 COMP 2406 CSC384 BBU4202 Stat 134 ECON41415 CSE1OOF CP2406 ICT501 ICT CSE 104 CSCI 2300 TAS 100 CSCI 3110 CMPE 223 CSC220 CPT105 CSCI 1110 CM3112 CSC8406 SE 3316A COMP1212 CVEN90063 ECS 32B COM1005 COMP124 FV2204 PROG2005 MA569 INFO151 COMP90038 CS4022 IS71083A COMP 424 COMP4033 EECS 1720 CS 2113 COMP1111 COMP212 INFR11199 COMP5911M ECON 5004 ECMM410 CSC B07 COMP 3430 CSB352 6CCE3ROB STAT5610 PUBPOL 522 COMP2610 FIT5227 BISY90009 COMP0083 NV 684 BUSML 3150 ECN21004 STAT6016 ELEC3705 MATH0033 CS5820 SCC311 CSci 4061 ECON 8820 INT104 ITE3713 CS551J ECM1410 CSMBD21 COMP 2012 CISC221 Code SCC312 COMP639 CMPSC 221 system COMP3217 COMP1721 ENG5056 Math 466 COMP0039 MFIN 5400F FINN40915 EENG31400 MODL5007M ​EEET 3050 EEET 3050 Quantitative Methods mathematics COMP1921 FIN3309 VE311 ESCI 1908 FIT5057 COSC2446 COMPUTING Math 110A EE 567 MATH10098 CISC642 EE10134 ECE 321 MTH2051 SIT 281 EEE3314 ELEC273 COMP5930M CE322 ELEC270 EE5101 MCEN90008 MTSC 887 Probability ENGN4528 MAE 424 MA2552 EBU5303 CHEM10600 EBU6018 ELEC2103 ELEE 5200 CSE 535 COMP6528 IS6153 IS3S664 BUSANA 7003 QTS0109 ECO3152B ENGR 227 LCSCI4208 MATH32051 ECS776P MGMT3004 N1551 JAVA ROB-6213 TNS3113 BEEM062 COMP47670 4SSMN903 BST 833 COEN 146 BASC0003 CAS EC501 Networks CSIT940 ELEC372 ACCFIN5034 Math 3527 DATA4000 INT102 FND109 MMM071 ROB6213 ETF5650 ECON 445 QMSS 301 Econ 320 PHY 4390 FIN 111 FINN41615 ECS 116 MTH6158 IOE 552 STA 141B Math 413 ECON3016 Physics 4303 Numerical BFF5270 EECS 111 FINANCE 251 COMP814 MGSC 410 ECON0051 EBU5376 STAT6118 ECON 20110 COMU7000 average acceleration BUSI4412 BFF3121 BIT233 ECMM462 ETC3430 DESN2348 INTE2584 ENME502 MA3XJ INTE2627 MA2815 MA3AM L0101 Math 3MB3 CPCCBC4004 EEEM061 0502E220 APPLIED 6SSMN310 ENV 3310 PM2PCOL3 CONS6201 MATH502 FIT5003 EEEN313 MATH3001 MECH3460 ECON30009 COSC1252 Assembler COMP 3023 ENGG7601 COMP20005 COMP SCI 1103 ICSI 402 INF2C CS320 COMPSCI7064 ECE 3220 PROGRAMMAMING MIPS Computer Science 2413 AM3611 MSOA TE2101 FFT CMPSC-121 CSE 109 COMP SCI 7064 HCI CMP-5013A CCN2042 COMP3400 EEEN30052 CO4215 EE101 KIT107 CSE 421 CSE521 MCD4720 EECS 280 MIT 403 GRPC VG101 APiE EECE 1080C FIT3143 CSE 325 ISOM 3029 CS3307 State SIT255 Engineering MQF Modelling ACX3150 SIA322 ACCT90004 COMU7201 MGMT90018 WRIT1000 COMP3702 BISM1201 COMP7505 IDEA9106 CSE3SMT BFC5926 BFC5280 BFC5935 QBUS3330 ECON3700 IFN521 ECON2121 COSC2626 MA413 DDES9903 ENGG1300 COMP9337 CO2201 ACCT2002 ICM289 MMM054 MSBA-204 DIGM707 CSC2250 Econ312 EVAT python CAN404 LUBS2840 CSCI-GA.2250 COMSM0093 COMP281 AFM 333 IBUS1001 CP2501 Math 105A VE320 TEC101 SOCY2166 COM240 EFIM20033 ENGI4467 EFIM20034 EC 979 BE432 7EJ502 CSSE6400 COMP90025 Econ 312 ENG2031 ECO0006 EXERSCI 207 CAN209 ECO 137W FT312 ECO 2199 MATH32052 BDW4213 APS 360 SAS 6 CHME0017 PO92Q Economics 01AV MATH39512 MATH 5486 COMP8620 ISE102 ECON235 ECON 206 FI 345 PHAY0020 MATH0099 MATH0085 EFB106 PHY 134 MAE115 circuits Chemistry CSE12 MATH-UA 233 PHAS0038 COMP2140 CONMGNT 7049 COMP151101 ECON 485 ACX5903 ENGN6536 ARCH1162 Law PHAS0042 CCF1C03 MATH 351 Phys 139 AG942 MGT001371 APH106 ECON1051 MA4AM MA3Z7 NUMBER THEORY REST0006 SESS0026 STAT0023 TABL 2741 CMP4008Y EFIM10015 Acct 560 PSYC735 GEOG 5 ACCT3104 CSEC5616 PHIL1012 ITLS6111 ECON8022 5CCM226A compX123 MA4XJ R001 EWB LLP120 COMP643 ENG 103 ECON 23950 ACCT 207 FINC 616 Bio99 Math 137A Psychology BCPM0054 MATH20212 EC3450 CENV6141 PSY 205 CE335 CS365 Calculus ACSD INFT6800 MCIT INFO6030 PHYS 111LV H63EEJ ECON2151 ENGI 2181 MTRX1701 PLIT08009 CS240 Math 270 CMP7000A CMP-7038B Math 263 LAW3016 CS371 STAT 334 FIN0008 ACC3004 STAT 371 ​COMP1921 MTH201 ACCT2000 UN3412 CIV6000 MATHS 3021 MATE7014 ECON1 CIBC6035 LAW121G COMM 321 CSC8204R TTM2033 CSCI 2600 MAE 115 LNG302 CENV6175W1 ECON30019 CPS2015 BST969 DDES9015 AMATH242 CS 1151 N1592 ACCT600 EG503G SMM519 EC318 Ecstatistics EEE 471 MARK2051 Topology COM00037H ACCT3000 MTHM501 EG501V COM00055H BUSN9085 GGR273 MATH 2B ITD102 MA214 ECON0060 ECE3114 ECMM447 Mechanics CCT361H5S BSAN3210 WELF2001 Fin3001 RESP5001 STA 137 Linguistics 101 CSCI368 CMPSC497 LUBS3655 OMBA 5355 BUSM2562 ​BFF5902 CYBR7001 CULT2005 ECON 7720 MTRX3760 FSE598 ​LUE1001 MGSC 7100 CS3240 COSC7500 ACCT3091 INFOGR TRAN 2080 DESIGN CIVE215001 CIVE2360 CPSC 8430 FNCE2003 Stoichiometry INFS6023 Quantitative Method Math 21D ECE5179 Design ​ECON8022 Chemical DMS 213 ADM1370 BFF5902 BFF2701 AGRI10051 AMN400 ECON7322 ​FINC5090 ​MATH1052 ​SciComp Elec4622 ​FINS5516 ENG 101 MMM143 CS431CA2 BSAN2201 EBSC7070 ES9v9-10 PLIN0009 DATA 8 MATH 101 BCPM0097 ​MAT 237 BISM2201 EEE8099 Physics 11 ECE2238B Biostat 234 ​ECON30009 INF10025 CHEM252 CCMA4008 CIVE 3007 STAT0031 ELEC ENG 3108 MGMT90140 CHEM 252 STAT3016 MMM095 ​MMGT6016 Legal STAT 311 ELEC9764 COMP 370 TCS 3053 EECS 1021 FIT1051 C/C++ EE3C COMP2003J COM398 COMP51915 Simulator FIN42330 8PRO102 PGD ELEC5160 XJCO1921 COMP5123M INFS 2042 CHE1148H ECA5313 IN3329 Microsoft Modeling B15 2TT COMP3687 COMP2432 DMS2030 KAN4TSF CFKG CSE 5322 CSE 445 STATS 3DA3 CHC5223 COMP1048 EL3105 EECS 3221 CS231 ME 4434 ITP4510 ITP4501 CSCI 5708 Controller EECE 5699 CPEN 231L CPN programs CSC8016 MATU9D2 ENGN4213
CONTACT US FOR
PROFESSIONAL HELP!
在线咨询
立即下单
首页 / essay创作 / essay润色精修 / homework & project / 网课托管 / 校园大使
联系我们CONTACT US
Wechat：THEend8_ Email：[email protected]
24小时全年无休客服
版权所有：Copyright 2014 Higher Education Group 本网站创作的所有文案及辅导内容均仅供参考 网站建设：海坤软件