

MTH2009
Complex Analysis
2023–24
Assessed Coursework Sheet 1
Please hand in your solutions via ELE by 12 noon on Friday 23rd February 2024. This assignment is worth 5% of your total mark for this module.
10 marks out of 100 will be for clarity (reasoning clearly expressed, correct use of notation, etc.) Please read the handout How to succeed in MTH2009 for guidance on this. In particular, start your answer to each question on a new page and leave plenty of space so that the marker can write comments.
(1) (10 marks) Verify the Cauchy–Riemann equations for the function f : C → C defined by
f(z) = πiz2 + eiz + √2.
(2) (15 marks) Find all complex solutions of the equation
z3 + 3z2 + (3 − 2i)z + 1 − 2i = 0
given that z = i is a solution.
(3) (15 marks) Let γ : [a, b] → C be a smooth path. Write down the formula for the length of γ. Using this formula, compute the length of the smooth path µ : [0, π/2] → C defined by
µ(t) = eit + t(sin t − i cost) + iπ.
(4) (25 marks) For a real number R ≥ 2 define γR : [0, π] → C by γR(t) = Reit . Prove that
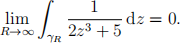
(5) (25 marks) Prove that the set
U = {z ∈ C : |Re(z)| < 2, |Im(z)| < 3}
is an open set. (You should not use the concept of boundary point in your proof.) Prove or disprove that U is a star domain.
- 经济Economics
- 金融Finance
- 会计Accounting
- 工商管理Business Management
- 计算机computer science
- 商业分析business analysis
- 法律Law
- 管理Management
- 市场营销Marketing
- 哲学Philosophy
- 心理学Psychology
- 物理Physical
- 统计学statistics
- 电气工程electric engineering
- 化学chemistry
- 生物biology
- 数学mathematics
- 语言学linguistics
- 土木工程civil engineering
- 工程力学engineering mechanics
- 艺术art
PROFESSIONAL HELP!
 Online consultation
Online consultation Place order online
Place order online



 Wechat:THEend8_
Wechat:THEend8_  Email:
Email: